9.1 邏輯閘 IC, 二元布林代代數學和數字電子技巧
專為模擬訊號而設計之運算放大器集成電路 (i) 可處理線性數學比例放大或 (ii) 非線性數學函數如積分、微分、振盪等。 電字邏輯閘IC (digital logic gate IC) 則全部設計為處理 (0 1) 二進位元而進行基於布林二元表達式 (binary Boolean expressions) 之數字計算。兩類電子元件屬於兩門完全不同電子科技範疇。它們發展起步時間相若,但電字邏輯閘IC很快便拋離運算放大器IC,發展成為更先進和更成熟電子科技。現時邏輯閘集成電路重要性遠高於線性集成電路 IC。
邏輯閘 IC 專門用在數字電路設計,應用範圍很廣。不但民用方面持續發展和增長,更在軍用和太空科技方面有不可取代之重要性。訊號數字 (碼) 化後產生遊離 (discrete) 高低訊號鏈,即 (0 1) 位元,其處理之可能性和方法極多,應用於多不勝數產品上,如智能手機、電腦、數碼相機、音響、電視機、廣告牌等等。昔日影像和聲音之播放只可以用模擬電路錄影帶和拾影/音磁頭,但現在錄影帶已在市場消失,取而代之是數字播放器。例如壓縮數字訊號 MP3、MPEG 4、JPEG、AVI、MK、FLV、DVD、MOV、WMV等解碼器,都需要邏輯閘集成電路始可運作。
(i) 數字 (二進位元組)邏輯和布林代數學 (Binary Boolean algebra and binary digital logic)
以十進數字 0 至 9 代入傳統代數方程式可得計算結果。但電子計算世界只有1 (高壓,5 V) 和 0 (低壓,0 V) 兩種數字,因此有需要建立另一種代數學,只能代入 1 和 0 兩個可能數字。這種代數學叫布林代數學 (Boolean algebra) 。
代入最簡單的傳統代數方程式 A + B = C,若A = 1, B = 2 即得 C = 3,若 A= 2, B = 3 則 C = 5,如此類推。若方程式以布林代數演繹,只可以寫作A + B = A 或 A + B = B。因所有布林變數只可以有 1 值或 0 值。若以電子電路演繹,就是一起兩端輸入 (0 0) 、(0 1) 、(1 0) 或 (1 1),因二進 (0 1) 比特有 22 或4種變化,輸出單端 1 或 0。布林邏輯衍生真值表 (truth table) (圖 237):
| A | B | A+B = A |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
| A | B | A+B = B |
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 1 | 1 |
(圖 237) Truth table
以上只是數學邏輯討論。要布林代數1值和0值與數字訊號產生聯動關係便需要電子電路去演繹,這類電路叫電子邏輯閘 (logic gate)。布林運算元 (Boolean operator) 之OR (+),AND (。) 或 NOT ( — ) 等皆可以電子邏輯閘演繹。
(ii) 電子邏輯閘 (Electronic logic gate)
電子邏輯閘有兩大類: (i) 早期之TTL (transistor-transistor logic) 和 (ii) 後來之CMOS (complementary metal oxide semiconductor) 。
各種電邏輯閘: | 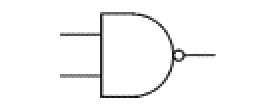 | 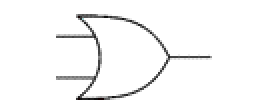 | etc | ||
AND | NAND | NOT | OR |
(iii) TTL電子邏輯閘
電晶體-電晶體邏輯 (Transistor-Transistor Logic,縮寫為 TTL) ,是開發和上市
較早的電子邏輯閘集成電路。顧名思義,TTL 每一單位以npn 雙晶體管直接耦合組成。常用零件編號為 74 xx 系列 (民用)。
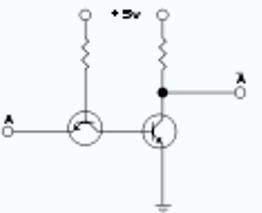
(圖 238) 一單位TTL反相器
如 (圖238) 所示,左邊npn晶體管發射極 (emitter) 作為輸入端 (A) 。只要接上髙壓 (5V) ,微少電流直通集電極 (逆向活性,reverse active mode) 。這電流啟動右邊 npn 晶體管基極 (base),通電至地,地和這枚npn集電極沒有電位差,令輸出端變為低壓 (0 V) 。當 (A) 端電壓變低,沒有電流通往右邊 npn 晶體管,地和這枚npn集電極之電位差為 5V,輸出端轉為高壓。結果這單位就是一反相器 (圖239)。
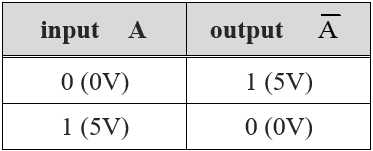
(圖 239) 圖238 之真值表
邏輯閘可以 是TT L 集成電路或 CMOS 集成電路,DIP 形式包裝,用作數字電
路電子零件。按線路接上各有關接點,完成設計之電路。一顆 DIP IC 內 (i) 有多個簡易相同邏輯閘,不會只有單一邏輯閘。例如 TTL 7404 就內置六組 NOT 邏輯閘 (圖 240) 。(ii) 多個複習而不同之邏輯閘如CMOS 4511 集成電路 (BCD to 7 segment) 內部結構則複雜得多 (圖 272) 。
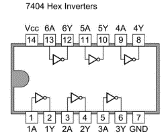
(圖 240) 7404 接腳分佈
(iv) 互補式金屬氧化物半導體 Complementary Metal-Oxide-Semiconductor (CMOS)
CMOS 是另一種消費者常用之集成電路的設計製程。在矽質晶圓模板上製出 NMOS (n-type MOSFET)和 PMOS(p-type MOSFET)的基本元件 (圖 241) ,由於 N MOS 與 PMOS 在物理特性上為互補性,因此被稱為 CMOS。

(圖 241) 一單位 CMOS 邏輯閘
CMOS 可用來製作靜態隨機存取記憶體 (RAM)、微控制器、微處理器、互補式金屬氧化物半導體圖像傳感裝置 (數碼相機感光元件) 和其他數碼邏輯電路系統。互補式金屬氧化物半導體具有只有在電晶體需要切換啟動與關閉時才需消耗能量的優點,因此非常節省電力且發熱量少,且製作上也是最基礎而最常用的半導體元件。CMOS 編號命名最常見的為 4xxx 系列。
TTL 與 CMOS 分庭抗禮。兩者相比較,TTL主要是速度快,CMOS 則是速度較慢但省電、成本比 TTL 低。隨着製造 CMOS 工藝進步,其反應度已經超越 TTL。而且 CMOS 內部不具有製作麻煩的電阻,TTL 一段時期可說沒有發展。目前 TTL 主要應用於教育或是較簡單的數碼電路。
TTL 與 CMOS 電源電壓,VDD或 Vcc,通常都是 5 V。但邏輯閘之1 (ON, 高壓) 和 0 (OFF, 低壓) 分辨電壓不一樣。兩者之閾值 (threshold) 電壓範圍,即啟動 CMOS 輸出1 之輸入電壓和啟動 CMOS 輸出 0 之輸入電壓和TTL不相同,不兼容。在同樣5V電源電壓情況下,COMS電路可以直接驅動TTL,但TTL電路則不能直接驅動CMOS电路。
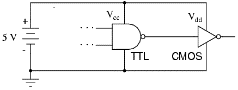
因此早期 TTL 和 CMOS 不可以如上圖般接連。但後期隨著新型品種 74HCxxxx (High speed CMOS) 和 74LS (Low power Schottky) 等推出市場,兼容問題基本上解決了。下圖 (圖 242) 簡單解析 CMOS NOT 邏輯電子閘 (inverter) 如何運作。TTL 和 CMOS 工作原理可於網上選閱。
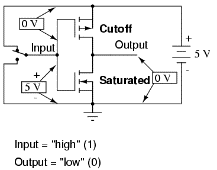
(圖 242) CMOS Inverter電子邏輯閘運作
市面可購買之邏輯電子閘集成電路均有編號。零件規格特性每間提供貨源之大廠,如早期之 FAIRCHILD 和現時之 MOTAROLA 或TEXAS INSTRUMENT (TI) 等皆印刷有關之手冊。每間大廠都擁有有關每一產品網上之專頁。
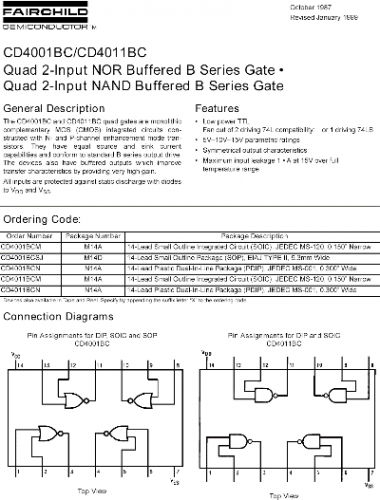
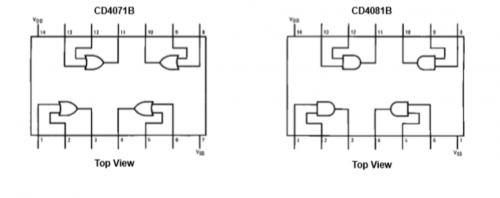
(圖 243) CMOS編號 CD 4001和 CD 4011之描述和接腳
CMOS 依布林代數邏輯組成不同電子邏輯閘去演繹7類二元布林運算元AND、NAND、OR、NOR、XOR、XNOR 和 NOT (即 INVERTER)。
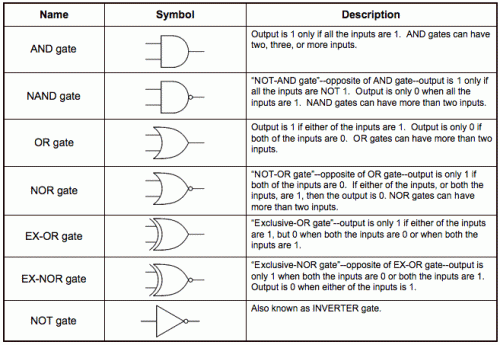
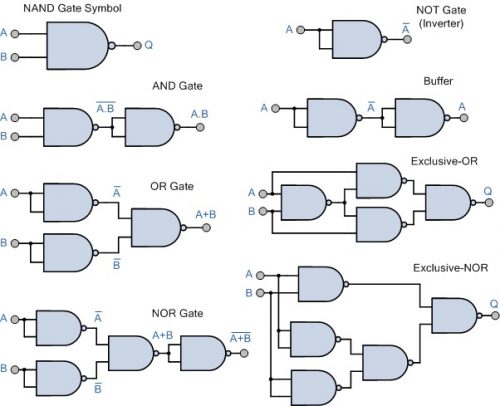
(圖 244) 7 種電子邏輯閘名稱,符號和簡介
其真值表如下 (圖245) :
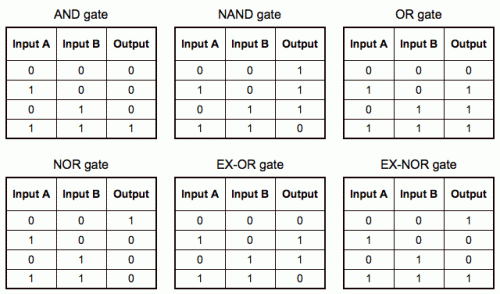 | INVERTER gate | |||||
|
(圖 245) 七種電子邏輯閘之真值表
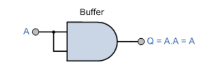
第七類電子閘不具邏輯運算,叫Buffer (緩衝器)。 0V 輸入0V 輸出 / 1V 輸入1V 輸出。作用是提高輸入阻抗,尤其耦合Op – Amp IC。
電子邏輯閘符號和真值表總結:
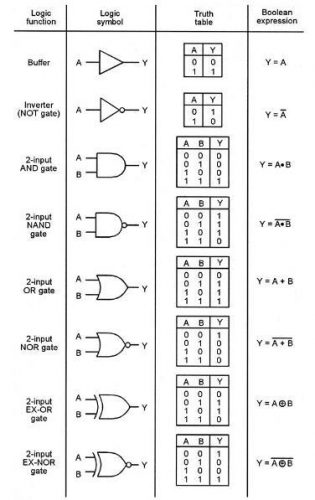
(圖 246) 各種電子邏輯閘符號和真值表
(v) 布林表式和真值表
布林表式 | 配合電子邏輯閘之真值表 |
A + B = A | 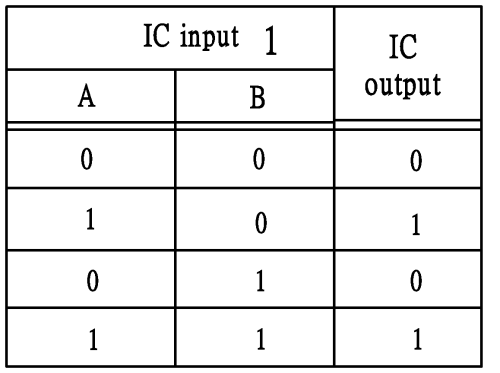 |
(圖 247) 布林表式 A+B = A 和相應之真值表
布林表式 | 配合電子邏輯閘之真值表 |
A + B = B | 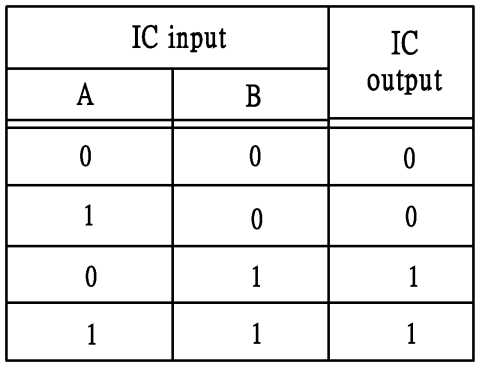 |
(圖 248) 布林表式 A+B = B 和相應之真值表
(vi) 布林代數邏輯,真值表和電子邏輯閘
STEM應用最深遠和影響極大就是二元布林代數運算元(binary Boolean algebraic expressions) 和電子邏輯閘數字計算 (logic gate digital computation) 互相之深度和複雜結合。完美體現STEM數學和科技於促進人類生活進步之偉大貢獻。
(a) 雙輸入二進位元 (A B)
回顧最簡單布林表式 A+ B = A 和 A + B = B,適當邏輯閘組合可以把它們結合起來,即直接轉數學為科技。以 4 個二進制位元只有 22 ,即4 種變化,(0 0) 、(1 0) 、(0 1) 、 (1 1) 代表布林方程 A + B = A 輸入一單位電字邏輯閘 (即 AND、NAND、OR、NOR等) 不可以取得 (0 1 0 1) 答案。只能以二單位耦合電子邏輯閘 (OR加AND) 運作,如以下顯示:
布林表式 | 真值表 | 電子邏輯閘組合 (AND加OR) |
A + B = A |  | 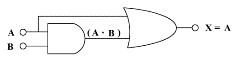 |
布林表式 | 真值表 | 電子邏輯閘組合(AND加OR) |
A + B = B |  | 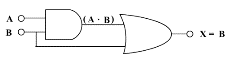 |
用 (OR連AND) 組合一樣可以:
| 布林表式 | 真值表 | 電子邏輯閘組合(OR加AND) |
| A + B = A |  | 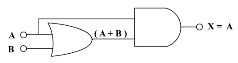 |
布林表式 | 真值表 | 電子邏輯閘組合(OR加AND) |
| A + B = B |  | 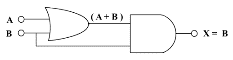 |
(1) 考慮一個不簡易例子:
A + B = 總是低壓 (i.e. 0)
很明顯,只用 AND 加 OR 組合 或 OR加AND 組合不滿足要求。我們嘗試加一非門 (NOT gate)
布林表式 | 真值表 | 電子邏輯閘組合(OR加NOT加AND) |
| A + B = 0 | 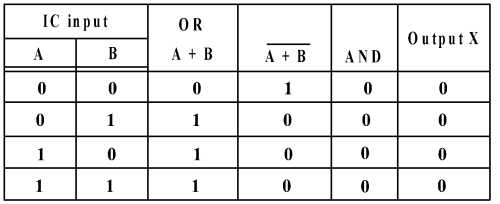 | 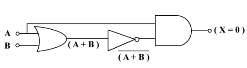 |
或 NOR加AND |
(2) 再考慮:
A + B = 總是高壓 (i.e. 1)
參考例子 (1),用NOR加NAND 便可以,自己試試。
(b) 三輸入二進位元 (A B C)
三輸入二進位元如 (A + B + C) 有23 或 8 種二進位元變化,即 (0 0 0)、(0 0 1)、(0 1 0)、( 0 1 1)、(1 0 0)、(1 0 1)、(1 1 0) 和 (1 1 1)。考慮下圖之邏輯組合:
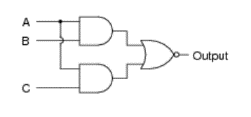
嘗試推算其二進布林表達式。
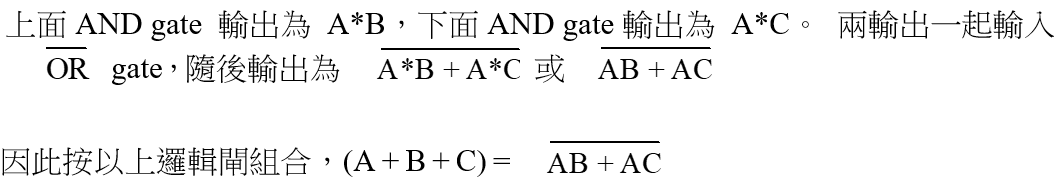
(c) 獨立和組合邏輯閘
先前陳述之7種二輸入二進位元邏輯閘 (圖 244, 245 和246) 每種不具必需性。每個邏輯閘既可獨立運作,也可由其他邏輯閘組合而成。因此,我們可以驗證基塊邏輯閘組合成某個邏輯閘,從而產生所有二進位元數字布林運算程式。
組合 (AND, OR and NOT) 稱為全組合元。其他4個邏輯閘,即NAND、 NOR、 ExOR 和 ExNOR (包括 buffer),都可以由全組合元或其中兩個構建而成,如下圖所示:
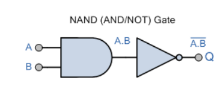 | 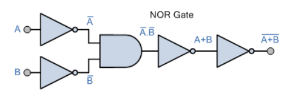 |
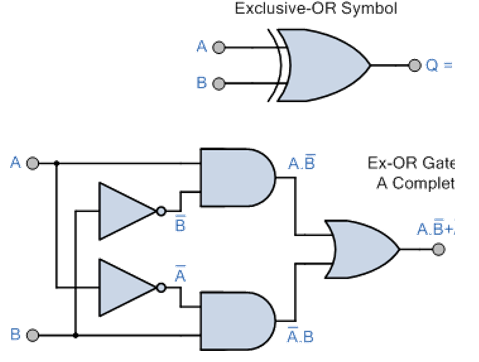 | 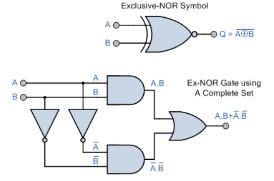 |
用單一邏輯閘構建全部7 種邏輯閘稱為基本元。NAND是基本元。只用 NAND 便可以構建全部7 種邏輯閘:
(d) 商 /民用邏輯閘晶片
CMOS 或 TTL 邏輯閘全部都以各類晶片出售,不用以晶體管或半導體親手裝組起來。 晶片垮國生產商如德州儀器 (TI)、摩托羅拉 (Motorola)、亞德諾半導體 (Analog Devices) 等經營多年,旗下生產民用晶片種類繁多,型號已標準化。個人電腦市場不斷發展,所用晶片如中央處理器 (CPU) 、接口設置 (interface device) 等型號則不停更新。電子線路設計沿用多年之COMS 4xxx 邏輯閘晶片是不會被淘汰的。邏輯閘封裝不只提供單一單位,全部封裝都有多個或混合單位。下圖顯示各標準型號CMOS輯閘晶片
CMOS IC | 描述 | CMOS IC | 描述 |
4081 | Quad 2-input AND | 4073 | Triple 3-input AND |
| 4011 | Quad 2-input NAND | 4023 | Triple 3-input NAND |
4071 | Quad 2-input OR | 4075 | Triple 3-input OR |
| 4001 | Quad 2-input NOR | 4025 | Triple 3-input NOR |
4070 | Quad Exclusive OR | 4082 | Dual 4-input AND |
| 4077 | Quad Exclusive NOR | 4012 | Dual 4-input NAND |
4000 | Dual 3-input NOR plus inverter | 4072 | Dual 4-input OR |
以上例子可見適當邏輯閘組合可以演繹基本布林表式A + B = A 或 A + B = B。 事實上,最複雜電腦硬件電路之原始計算步驟就是決定二進 (0 1) 位元狀態之輸出是 0 或是 1。簡單地總結如下

(e) 一個實用但相當複雜的四輸入二進位元 (A B C D) 例子
一個常見,但很複雜的例子便是硬件電路之BCD(二進位編碼的十進位)計數器顯示。下列三表格概述如何用四顆 LED 隊列顯示十進 0 至9 數字。電路涉及複雜軟件式二元布林邏輯運算。不過應極大供求需要,晶片廠商把整個複雜編程數字邏輯化,製成集成晶片推出市場。這就是以下介紹 IC CD 4510之起因。
要求 | 真值表 |
基於邏輯閘組合,設計一數字線路顯示十進 0 至9 數字。 兩顆二進制位元LED 隊列可顯示22 或 4 種可能性,即0 至 4 數字,不達要求。 四顆二進制位元LED 隊列可顯示24 或 16 種可能性,不獨可以顯示 0 至 9 數字,也可以顯示其他字母和符號。這種數字名命叫十六進制。 要有一時鐘,輸出鎖定頻率方波脈衝訊號鏈。 二進制四位元 (A B C D ) 真值表匹配十進數字輸入,四位元 (A B C D ) 輸出。 | 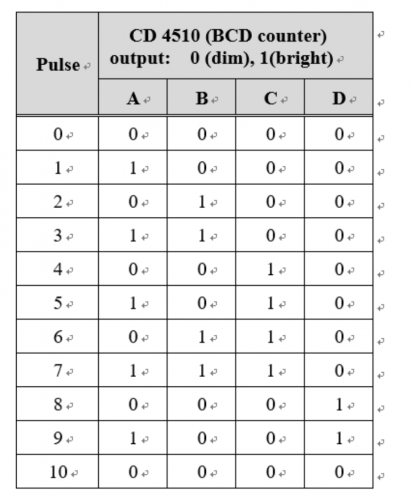 |
邏輯閘線路 | ||
實現要求需要一複雜邏輯閘組合線路。 # 0顯示為 (0 0 0 0 ),4顆LED隊列顯示為 (暗 暗 暗 暗), # 1顯示為 (1 0 0 0 ),4顆LED隊列顯示為 (光 暗 暗 暗), # 2顯示為 (0 1 0 0 ),4顆LED隊列顯示為 (暗 光 暗 暗) 如此類推。 適用之邏輯閘組合電路是市面有售之 BCD 4 bit計數器 IC CMOS CD 4510。其複雜內部結構如下圖所示。 | ||
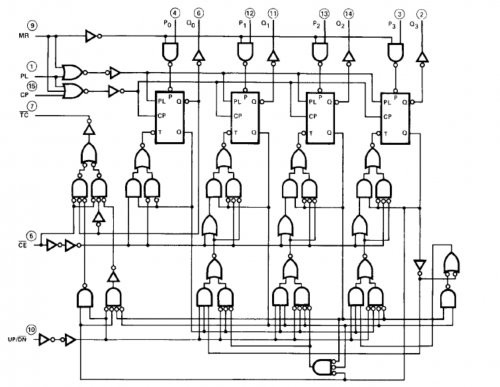 |  | |
CMOS CD 4510 BCD 4 bit計算器 | ||
| CD 4510 IC計數器為一通用數字集成電路,接腳可接各種數字運算訊號。但目前工作只考慮輸入脈衝方波 (時鐘) 和輸出4位元 (A B C D 或 Q0 至Q3 ),因此第1、3、4、5、8、12和第13腳全部連接地。其他接腳,如第16腳 (VDD) 接 + 9V,第 9 腳 (重置) 通過 10K 電阻接地,第10腳接 + 9V,第 15腳接 555 IC無穩態複振器輸出 (IC第 3腳) 約 3 Hz方波脈衝 (時鐘) 。第 (2、6、11、14) 腳分別以4位元 (A B C D ) 輸出。下圖顯示於麵包板接駁之線路。主題 9.3 (數字頻率顯示器) 有較詳細閘述 CD 4510計數器功能。 | ||
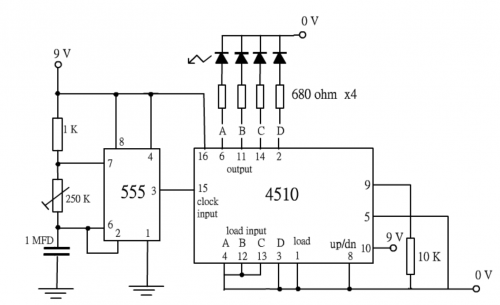 | 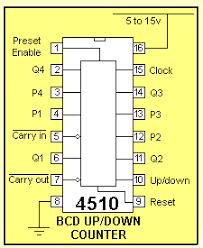 | |
以下短片說明0 至9 數字如何由四顆 LED隊列麵包板上順序顯示。
CD 4510 BCD 4 bit output
習作 (11 ) :設計以 CMOS CD 4071 (Quad 2-input OR gate,四2輸入端或門) 和 CD 4081 (Quad 2-input AND gate,四2輸入端和門) 邏輯閘數字電路驗證布林表式A + B = B
物料:CD 4071, CD 4081, 麵包板,4.5 V 電源,LED,100 K 電阻 (若要LED 亮些,可降低阻值,如 50 K),接線,三刀四擲選擇器。
|
步驟:(1) 按下圖線路完成接駁。
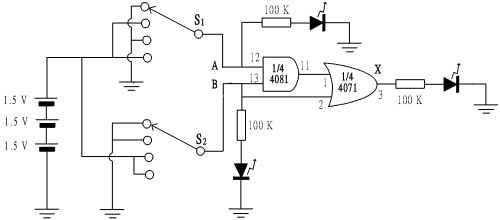 | 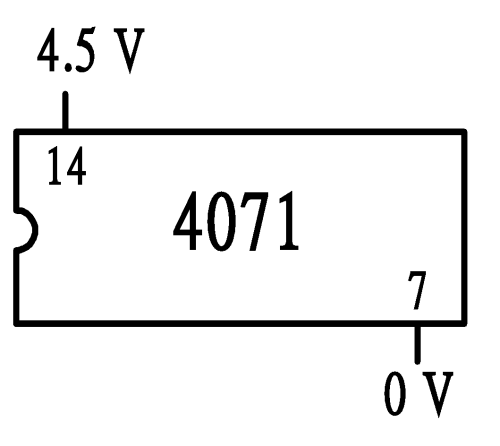 |
 |
(圖 249) 布林表式 A+B = B 和相應之電子閘電路
(2) 轉動三刀四擲選擇器旋鈕令 (A, B) 按 (0 0),(0 1),(1 0) 和 (1 1) 變化。觀察輸入端A,B和 輸出端 X LED亮度。
 |  |  | ||||||
線路實物圖 | 三刀四擲選擇器(只用其中兩組) |
|
 |  |  |
|
|
| ||||||||||||||||||
(圖 250) A 和 B 端連續輸入 (0 0),(1 0),(0 1) 和 (1 1) 顯示 X 輸出端
A + B = B
何時選擇數字訊號以 A + B = A 運算,何時選擇數字訊號以 A + B = B 運算?這方面需要數據選擇器 (multiplexer)。數據選擇器邏輯電路之真值表為
S | A | B | Q | |
0 | 0 | 0 | 0 | A + B = A |
| 0 | 0 | 1 | 0 | |
0 | 1 | 0 | 1 | |
| 0 | 1 | 1 | 1 | |
1 | 0 | 0 | 0 | A + B = B |
| 1 | 0 | 1 | 1 | |
1 | 1 | 0 | 0 | |
| 1 | 1 | 1 | 1 | |
當 S 為 0 時,數字訊號 A和 B 輸入以 A + B = A 運算,結果 Q = A。當 S為 1 時,數字訊號 A 和 B 輸入以 A+ B = B 運算,結果 Q = B。以上可看成是 A+ B = A 或 A+ B = B 運算之擴張真值表。可以說是數字電路理論香農展開 (Shannon’s expansion) 於 2 選 1 數據選擇器之最簡化演繹。
數據選擇器有自身符號 (圖 251)。2 選 1 電子選擇器可比喻為一手動單刀雙擲選擇器 (圖 252)。這類集成電路也稱三態邏輯閘。
|  |
| ||||||||
2 選 1 電子選擇器 | 比喻為一手動單刀雙擲選擇器 | 香農展開真值表 |
(圖 251) (圖 252)
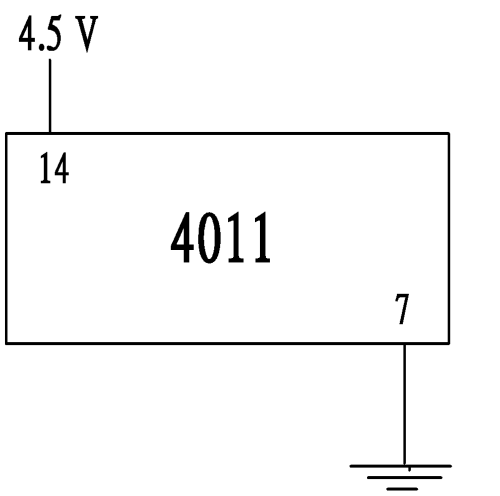
習作 (12):設計以 CMOS CD 4011 (Quad 2-input NAND gate,四2輸入端與非門) 邏輯閘數字電路模擬布林表式 A+ B = A 或 A + B = B 2 選 1
|  | |||||||||||||||||||||||||||||||||||||||
物料: CD 4011,麵包板,4.5V 電源,LED,100 K 電阻 (若要 LED 亮些,可降低阻值,50 K),接線,三刀四擲選擇器,單刀二擲選擇器
步驟:(1) 按下圖線路完成接駁。
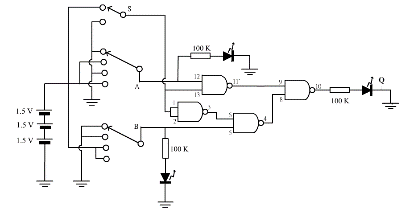 |  |
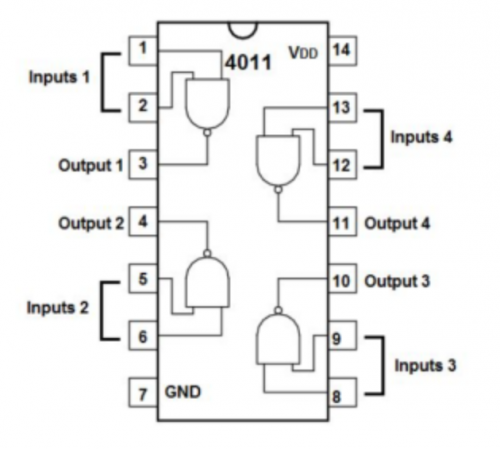 | |
(圖 253) A + B = A 或 A + B = B 2 選 1 線路 |
(2) 轉動單刀二擲選擇器旋鈕 S 令 IC 第 13 腳接 0V,即 S = 0。
(3) 轉動三刀四擲選擇器旋鈕。
(4) 選 (A B) 為 (0 0) ,記錄 LED Q 亮度。
(5) 選 (A B) 為 (1 0) ,記錄 LED Q 亮度。
(6) 選 (A B) 為 (0 1) ,記錄 LED Q 亮度。
(7) 選 (A B) 為 (1 1) ,記錄 LED Q 亮度。
(8) 調校 S 接 4.5 V,即 S = 1。重複以上步驟。
結果:完成下表
S | A | B | LED Q亮度 (光 = 1,暗 = 0) | |
0 | 0 | 0 | A + B = ( ) | |
| 0 | 1 | 0 | ||
0 | 0 | 1 | ||
| 0 | 1 | 1 | ||
1 | 0 | 0 | A + B = ( ) | |
| 1 | 1 | 0 | ||
1 | 0 | 1 | ||
| 1 | 1 | 1 | ||
(vii) 頻率計數器 (Frequency counter)
實用電腦數字電路當然不會使用手動選擇器來轉換眾多執行指令。任務交予數據選擇器和時鐘。習作 (12) 只是一個模擬數據選擇器運作線路,真實數據選擇器應用則複雜得多 (網上自修) 。數據選擇器需要外接時鐘產生一連串開 ((1), 5V)/關 ((0), 0V) 脈衝訊號鏈始可運作。時鐘提供時基作數字運算,時鐘通常指計數器 (frequency counter)。電腦硬件計數器採用晶體壓電效應物料 (piezo electric material),例如石英 (quartz) 產生精準振盪方波脈衝訊號鏈,可達至10-9 秒分辨準確度。時鐘越快,準確度越高。一般用途振盪頻率幅度為數Hz至 數千 Hz,用不著使用石英振盪。運算放大器耦合RC電路作無穩態複振器 (弛張振盪器) 、CMOS反相邏輯閘耦合電容起振器或是專門為振盪而設計之IC如555都非常合適。
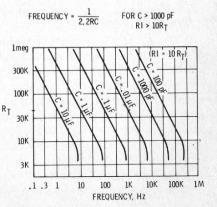
Op-Amp 弛張振盪電路 (圖 228) 為廣泛採用之無穩態複振電路,主題 8.3 已有所討論。CMOS 無穩態複振電路有多款,下圖 (圖 254) 以 CD 4049 反相邏輯閘 IC 起振之方波頻率為 f = 1/2.2 RC。當 R = 100,000 W 和C = 0.001 x 10-6 F,
f = 1/(2.2 x 100,000 x 0.001 x 10-6) Hz 或 4545 Hz。
若考慮計算誤差、電阻阻值和電容數值誤差,可接受之實值為計算值 (+/-) 15 %,上述例子則為 4545 (+/-) 682 Hz。
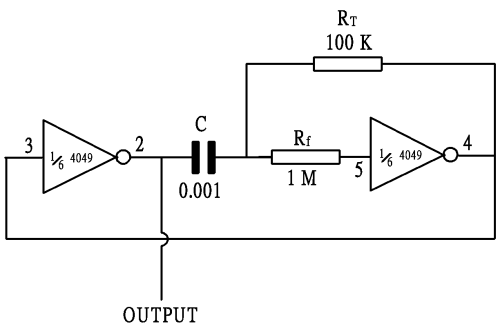 |
(圖 254) CD 4049 反相器 IC 起振器
(圖 255) CD 4049 起振器產生5130 Hz方波 |
(viii) 失真模擬訊號數字化
訊號數字化一個主要用途是消除和訊號一起的雜訊 。當沒有雜訊模擬波動電壓輸入電子邏輯閘反反相器 (即輸入 0 輸出也是 0, 輸入 1 輸出也是 1,也稱緩衝器,buffer) 預設一閾值電壓,便可轉換為 (0 1) 位元。下圖 (圖 256) 可見若輸入模擬訊號電壓高於閾值電壓,數字訊號輸出保持於高壓,即 +5V或 (1) 。 當輸入模擬訊號電壓低於閾值電壓,數字訊號輸出即時變為低壓,即 0 V或 (0) , 並保持於這數值。(紅線為數字訊號電壓,綠色曲線為波動之沒有雜訊模擬訊號電壓)。
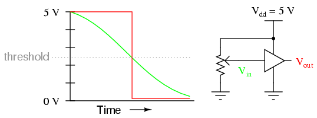
(圖 256) 模擬/數字轉換閾值電壓
若模擬訊號有雜訊,(0 1) 數字訊號位元將會不一樣。如果把緩慢改變疊有雜訊之DC 模擬訊號 (綠色),即失真模擬訊號,轉換為數字訊號 (紅色),閾值電壓會有三交叉點而不是只有一交叉點,結果有兩個數字脈衝而不是只有一個 (圖 257)。
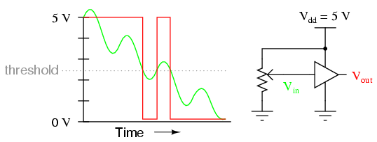
圖 257) 閾值電壓出現三次,緩衝器數字訊號輸出不一樣
解決方法是用一類電路叫施密特觸發器 (Schmitt trigger),整個線路以下圖為符號:
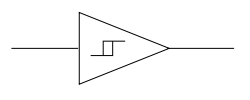
上圖正中圖案代表遲滯現象 (hysteresis),用來顯示鐵磁物料之 B-H 磁滯曲線。施密特觸發器之組合為一運算放大器接駁成比較器及在非反相輸入端作正回饋並設下兩閾值電壓,一高一低。由低閾值電壓和高閾值電壓激發之數字位元 (0) 和 (1) 及期間之時差都決定於模擬訊號之變化。這種往返機制跟遲滯現象很相似。
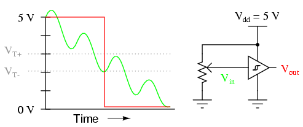
(圖 258) 失真模擬訊號用施密特觸發器數字化後呈正常脈衝
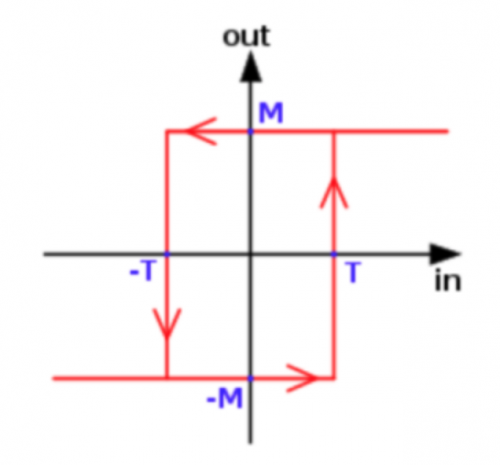
施密特觸發器示意圖 (圖 259). OX 和OY 軸分別為輸入和輸出電壓。 T 和 −T 為轉換閾值電壓,M 和 −M 為輸出數字電壓。當輸入電壓 (T) 高於高閾值電壓,輸出數字電壓為 +5V (M) 並維持此值。若輸入電壓下降至低閾值電壓 (-T),輸出數字電壓即時變為0V (-M),並維持此值。重複此模式出現如一B-H 磁滯曲線 (圖 259)。 |
(圖 259) 施密特觸發器轉換曲線 | ||
讀者若想了解施密特觸發器詳細資料,可上網頁閱覽。
9.2 硬件、軟件、二進制位元,位元組、數字運算和個人電腦 (PC)
(i) 硬件與二進制數字運算
電腦硬件為一套有物理形狀、可觸摸、複雜的電子和機械設備,包括機殼、中央處理器 (CPU)、顯示器、鍵盤、儲存器、graphics 卡、sound卡、揚聲器和主板 (motherboard)。電腦硬件運作需要啟動內置操作系統 (operating system, OS) 和輸入一組有數字邏輯的二進制位元組指令,即軟件。
二進 1 位元 (1 bit) 有 21 即 2 種變化 0 和 1,實際電子用途只可以說是一個開關制處於接通 (即 1) 和關 (即 0) 狀況。二進 2 位元 (2 bit) 有 22 ,即 4 種二進制變化 (0 0),(0 1),(1 0) 和 (1 1)。實際電子用途只是作為二進制 (binary bit) 位元,廣泛地用於各系列電子計算機 (電腦) 數字運算。二進 3 位元 (3 bit) 有23,即 8 種二進制變化 (0 0 0)、(0 0 1)、(0 1 0)、( 0 1 1)、(1 0 0)、(1 0 1)、(1 1 0) 和 (1 1 1)。實際電子用途不如2位元普遍。近年有學者嘗試用二進3位元把易經之乾坤八卦和六十四卦作電子運算演繹 (可上網搜尋,也可想像占卜龜殼內之三枚銅錢,代表天、地、人),超越數字、圖形和符號範疇。二進 4 位元 (4 bit) 有 24 ,即16 種二進制變化。實際電子用途是作為十六進制 (hexadecimal) 和鍵盤符號普遍採用的拉丁語系ASCII (American Standard Code for Information Interchange) 制式之標準。
第一代數字計算概念源於二進制4 bit 位元 。4 bit 位元可如下表 (圖260) 分配二進、十進和十六進制進行運算。
Display | |||
| Binary | Octal | Decimal | Hexadecimal |
0000 | 0 | 0 | 0 |
| 0001 | 1 | 1 | 1 |
0010 | 2 | 2 | 2 |
| 0011 | 3 | 3 | 3 |
0100 | 4 | 4 | 4 |
| 0101 | 5 | 5 | 5 |
0110 | 6 | 6 | 6 |
| 0111 | 7 | 7 | 7 |
1000 | 10 | 8 | 8 |
| 1001 | 11 | 9 | 9 |
1010 | 12 | 10 | A |
| 1011 | 13 | 11 | B |
1100 | 14 | 12 | C |
| 1101 | 15 | 13 | D |
1110 | 16 | 14 | E |
| 1111 | 17 | 15 | F |
(圖 260) 4-bit位元組和各進位元採用之顯示
二進制 4 bit 電子運作不可以語言化,即不足以分配十進位阿拉伯數目字 0 至 10,英文 26 個字母 A 至 Z 和其他常用之符號。二進制8 bit有 28 即 256 種變化,可分配十進數字 0 至 10,英文 26 個字母 A 至 Z 和常用顯示之符號如 =、>、<、/、@ 等之 ASCII 字元集 (圖 261, 262)。指令電腦硬件運作需要程式語言編寫程式,即軟件。
機器可以解碼以二進制4 bit編寫之程式,但它不可以按人類語言規範作指令運算。換句話說,這類初階程式編寫很有局限性,不可以以人類語言編寫,故稱之為「機械語言」(machine language)。以二進制8 bit,或1位元組編寫之程式基本上可認識人類常用之語言字彙為指令規範,衍生初期極為普及之BASIC,FORTRAN等程式。

(圖 261) 盤主板之ASCII字元符號
ASCII 的局限性在於只能顯示 26 個基本拉丁字母、阿拉伯數目字和英式標點符號,因此只能用於顯示現代英語或美式英語。後來發展了「統一碼」(Unicode),可用於其他語系。ASCII字元集普遍地用於鍵入程式編寫,其簡易 user-Friendly 程度很為人們接。(網上鍵入關鍵詞 (ASCII)可得較詳細資料)
Binary | Decimal | Hexa decimal | Graphic | Binary | Decimal | Hexa decimal | Graphic | Binary | Decimal | Hexa decimal | Graphic |
0010 0000 | 32 | 20 | (space) | 0100 0000 | 64 | 40 | @ | 0110 0000 | 96 | 60 | ` |
| 0010 0001 | 33 | 21 | ! | 0100 0001 | 65 | 41 | A | 0110 0001 | 97 | 61 | |
0010 0010 | 34 | 22 | “ | 0100 0010 | 66 | 42 | B | 0110 0010 | 98 | 62 | b |
| 0010 0011 | 35 | 23 | # | 0100 0011 | 67 | 43 | C | 0110 0011 | 99 | 63 | |
0010 0100 | 36 | 24 | $ | 0100 0100 | 68 | 44 | D | 0110 0100 | 100 | 64 | d |
| 0010 0101 | 37 | 25 | % | 0100 0101 | 69 | 45 | E | 0110 0101 | 101 | 65 | |
0010 0110 | 38 | 26 | & | 0100 0110 | 70 | 46 | F | 0110 0110 | 102 | 66 | F |
| 0010 0111 | 39 | 27 | ‘ | 0100 0111 | 71 | 47 | G | 0110 0111 | 103 | 67 | |
0010 1000 | 40 | 28 | ( | 0100 1000 | 72 | 48 | H | 0110 1000 | 104 | 68 | h |
| 0010 1001 | 41 | 29 | ) | 0100 1001 | 73 | 49 | I | 0110 1001 | 105 | 69 | |
0010 1010 | 42 | 2A | * | 0100 1010 | 74 | 4A | J | 0110 1010 | 106 | 6A | j |
| 0010 1011 | 43 | 2B | + | 0100 1011 | 75 | 4B | K | 0110 1011 | 107 | 6B | |
0010 1100 | 44 | 2C | , | 0100 1100 | 76 | 4C | L | 0110 1100 | 108 | 6C | l |
| 0010 1101 | 45 | 2D | – | 0100 1101 | 77 | 4D | M | 0110 1101 | 109 | 6D | |
0010 1110 | 46 | 2E | . | 0100 1110 | 78 | 4E | N | 0110 1110 | 110 | 6E | n |
| 0010 1111 | 47 | 2F | / | 0100 1111 | 79 | 4F | O | 0110 1111 | 111 | 6F | |
0011 0000 | 48 | 30 | 0 | 0101 0000 | 80 | 50 | P | 0111 0000 | 112 | 70 | p |
| 0011 0001 | 49 | 31 | 1 | 0101 0001 | 81 | 51 | Q | 0111 0001 | 113 | 71 | |
0011 0010 | 50 | 32 | 2 | 0101 0010 | 82 | 52 | R | 0111 0010 | 114 | 72 | r |
| 0011 0011 | 51 | 33 | 3 | 0101 0011 | 83 | 53 | S | 0111 0011 | 115 | 73 | |
0011 0100 | 52 | 34 | 4 | 0101 0100 | 84 | 54 | T | 0111 0100 | 116 | 74 | t |
| 0011 0101 | 53 | 35 | 5 | 0101 0101 | 85 | 55 | U | 0111 0101 | 117 | 75 | |
0011 0110 | 54 | 36 | 6 | 0101 0110 | 86 | 56 | V | 0111 0110 | 118 | 76 | v |
| 0011 0111 | 55 | 37 | 7 | 0101 0111 | 87 | 57 | W | 0111 0111 | 119 | 77 | |
0011 1000 | 56 | 38 | 8 | 0101 1000 | 88 | 58 | X | 0111 1000 | 120 | 78 | x |
| 0011 1001 | 57 | 39 | 9 | 0101 1001 | 89 | 59 | Y | 0111 1001 | 121 | 79 | |
0011 1010 | 58 | 3A | : | 0101 1010 | 90 | 5A | Z | 0111 1010 | 122 | 7A | z |
| 0011 1011 | 59 | 3B | ; | 0101 1011 | 91 | 5B | [ | 0111 1011 | 123 | 7B | |
0011 1100 | 60 | 3C | < | 0101 1100 | 92 | 5C | \ | 0111 1100 | 7C | ||
| 0011 1101 | 3D | = | 0101 1101 | 93 | 5D | ] | 0111 1101 | 125 | 7D | ||
0011 1110 | 62 | 3E | > | 0101 1110 | 94 | 5E | ^ | 0111 1110 | 126 | 7E | ~ |
| 0011 1111 | 63 | 3F | ? | 0101 1111 | 95 | 5F | _ |
(圖 262) ASCII字元符號
當我們按下電腦鍵盤其中一鍵時 (俗稱單擊),若採用10-bit字符架構,鍵盤即時輸出一start bit (low),跟着一8 bit 數據位元, 一stop bit (high)。例如單擊A鍵,屏幕見「A」字。按 (圖 262, ASCII 字元符號) 所示,輸入二進制數據位元組為 (0100 0001)。電腦運算 (0100 0001) 位元組,光柵掃描 (Raster scan) 並以8 x 8 像素格柵矩陣圖形屏幕顯示「A」(圖 263)。可見一簡單動作其實已經進行了一連串複雜執行指令。鍵盤運作機理就是用一種user-friendly和簡單方法達至與電腦互動。
 |
Character “A” in 8x 8 Matrix by Raster Scan |
(图 263) (0100 0001) 位元组屏幕矩陣圖形顯示為「A」
(ii) 程式語言與軟件
(a) 民用和商業軟件
程式語言(programming language),是用來定義電腦程式的形式語言。它是一種被標準化的交流技巧,用來向電腦發出指令。電腦語言讓程式設計師能夠準確地定義電腦所需要使用的數據,並精確地定義在不同情況下所應當採取的行動,不可以有絲毫錯誤。程式語言有低階和高階之分,發展也有先後。低階語言指令普通人解不通,只供機械認識,因此叫機械語言 (machine language)。高階語言以人類的日常語言為基礎的一種程式語言,使用一般人易於接受的文字來表示,以方便對電腦認知較淺的人亦可以大概明白其內容。
高階語言指令早於上世紀50年代已開發,其後流行使用的先有數學科應用之FORTRAN (FORmula TRANslator)、商業用的 COBOL (COmmon Business Oriented Language) 、通用之BASIC (Beginner’s All-purpose Symbolic Instruction Code) 和辦公室用之LOTUS – 123 試算表等軟件 (spreadsheet)。試算表之應用是與電腦互動,功能以表格形式組織、分析和儲存數據。以上程式語言早期只供大型電腦 (mainframe) 使用。後來因個人電腦 (PC,personal computer) 開發,中央處理器 (CPU) 廣泛應用及運作速度飛躍發展,程式語言變得日新月異。現時最受歡迎之程式語言有Java、C#、Python、Ruby 等。
軟件是一系列按照選用程式語言和特定顺序組織的電腦数據編程和指令,是電腦中的非有形部分。硬件之核心組件中央處理器 (CPU),發展飛躍,而配合之軟件和作業系統也日新月異。上世紀70年代初期個人電腦作業系統 (Operation System, OS) 全部使用 DOS (Disk Operating System) 當時流行之英文文書軟件有 「WordStar」 和 「Word Perfect」。 因 DOS 指令不淺白,並不user-friendly,所以後來被以桌面檔頁圖標 (icon) 和滑鼠 (mouse) 為賣點操作簡易之微軟「視窗」(Windows) OS全面取代。編寫多個最初版本「視窗」之程式語言為Visual Basic 和 Visual Basic. NET。最新「視窗 10」 版本 OS則用C作基礎,後來加入更高階程式語言如C#、CPP 或 Pytho。微軟著名軟件為文書用經常更新之捆綁式 「Office」,初期版本內有文書用之 「Word」、 試算表 「Excel」、 演講顯示用之 「PowerPoint」 和 電郵用之「Outlook」。後來加入「OneNote」、 「OneDrive」和視像傳輸用之「Skype」。
(b) 工業軟件
廣泛地說,處理工程、礦業、化工、能源等範疇製造業資訊之軟件謂之工業軟件。工業軟件可處理評估、職業成本、製作之會計,經營或安排、專業物料設計,生產程序解決方法等。
MATLAB 捆綁Simulink 是工程界廣用之軟件 。MathWorks 開發MATLAB (“matrix laboratory”) 。軟件具多功能性質,可作矩陣運算、圖解函數和數據、實施演算法、創建用者介面與其他編寫程式連結。至 2020年,全球有多於 400 萬用家。MATLAB使用者具工程、科學和經濟等專業經驗。大有名堂之 AutoCad、CorelRAW、Photoshop 軟件已廣受設計藝術家歡迎數十載。
(c) 移動智能手機軟件應用 (Apps, Software Applications)
步入千禧年代,互聯網應用極之普及。智能手機已是個人日常之必需品。目前智能手機軟件 (或稱 Apps) 之作業系統源碼不是iOS就是Android,但都需要使用移動程式語言。不像桌上電腦「視窗 10」OS程式語言主要有 C,C++ 和C#,流動電話之移動程式語言有多款,包括Java、 Javascript、 C#、 C++、 Python、 PHP 等,全部支援Internet Explorer (IE), Google, Chrome和Firefox 瀏覽器。
(d) 「雲端」運算
「雲端」為一比喻詞,沒有實質意思,可理解為超區域運作,如浮雲一樣。「雲端」運算近年興起,但不視作一發明產業。「雲端」服務指透過互聯網提供各類承索服務,或「一經要求,即可使用」之服務設施。「雲端」電腦系統資源儲存於大型遙遠數據庫,不需用者自行管理。不論以太網絡 (ethernet) 桌上電腦或是其他接收速度和記憶體足夠之移動電子裝置,只要能上互聯網,都可以如下圖般接觸 「雲端」服務。
主要「雲端」服務有:
* 電郵收發
* 數據儲存、備份、數據檢索
* 編寫和檢測 Apps
* 分析數據
* 影音串流 (Audio and video streaming)
* 提供軟件
廣義地說,有三類「雲端」服務: (i)「軟體即服務」(Software-as-a-service, SaaS) ,(ii)「基礎設施即服務」(Infrastructure-as-a-service, IaaS) 和 (iii)「平台即服務」(Platform-as-a-service, PaaS) 。SaaS 有銷售授權用家自行網上安裝軟件如微軟「Office 2016」和「Office 365」,有別於傳統 CD-ROM 微軟Office軟件。IaaS有自行選擇伺服器, PaaS 則可尋找自我宣傳之網頁設計平台。
「雲端」服務甪者可由Dropbox或Google Drive在不同電腦檢視、發放或儲存電郵。時下流行手機拍攝後Instagram上「雲端」儲存或檢索。「雲端」之高流動性尤其適用於人工智能應用,例如物聯網 (IoT) 、無人駕駛、無人機、機械人等。
免費網上電郵服務如 Gmail、Yahoo mail和Hotmail 由瀏覽器提供,有別於「雲端」服務。
(iii) 二進制位元組架構跳躍式發展
雖然 8 bit位元組程式數字字句可轉換為鍵盤 ASCII字元輸入,但8 bit位元組是中央處理器基本上可以處理之數字位元組,遠遠達不到 CPU 運作速度隨時間增加而作對數式倍增之要求。因此 2 位元組 (16-bit)、 4 位元組 (32-bit) 和現時起步之8 位元組 (64-bit) 數字字句程式相繼出現。相關之程式語言也變得五花八門。讀者可再參閱網頁得較詳盡之有關資料。
總結數字電子之開拓和發展,證明數學 (布林代數學) 和科技有唇齒相依不可分離關係。數字電子應用之深度廣泛就是 STEM空前成功的一個極好例子。
9.3軟件和硬件正向/逆向工程 (基於網上資料)
(i) 軟件正向/逆向工程
顧名思義,正向工程是由原料至產品的工序。逆向工程則是另一種技術過程,即對一專案產品進行逆向分解,分析及研究。從而演繹並得出該產品的處理流程、組織結構、功能效能規格等設計要素,以製作出功能完全一樣的產品,或進一步提升該產品效能。
軟件原始碼 (source code), 指令 (instruction), 編譯代碼 (compiled code) 和 二進目標代碼 (binary object code)
軟件和硬件一定要精準耦合才可使一台電子計算機正常運作。以外行人而言,就是軟件命令硬件何時和如何工作。要一窺全豹,可從軟件起始一步一步技術性地跟進,到硬件落實執行。這過程稱軟件正向工程。
計算機正向工程由決定採用某一程式語言開始,跟著配合電腦 OS編寫一沒有錯誤之程式。舉例用C語言編寫屏幕顯示方程式 3 + 8 = 11 如下:
Line | |
1 | #include |
2 | |
3 | int main() |
4 | { |
5 | int a, b, c; |
6 | a = 3; |
7 | b = 8; |
8 | c = a + b; |
9 | printf(“%d + %d = %d\n”, a, b, c); |
10 | return 0; |
11 | } |
標頭檔 (standard input output as header) 為C 語言指令,理解為從鍵盤標準輸入並以屏幕標準輸出。第三行int main() 宣示主要功能。這些全部指令稱作原始碼 「source code」。電腦硬件主體不識辨別C 語言或其他高階語言編寫之程式,只接受0 (0V) 或1 (5V)之二進制比特脈衝訊號。有需要用一編譯器 (complier) 把高階語言轉為低階語言如匯編語言 (組合語言,assembly language)、目標代碼 (object code) 或二進制機械語言 (binary machine language),產生令硬件可執行之程式。整體結果是把一大堆0 和1二進制比特以位元組 (字節,byte) 或 字組 (word) 精準地和非常有條理地匯入硬件各組件輸入埠,進行繁複電子邏輯閘運算。
如想修改程式顯示5 + 7 = 12,只要改a為5,b為7便可以了。若遺失了原始碼,便要從新辨清用可種語言,重組編寫或優化程式。這就是軟件逆向工程。不過複雜軟件程式之原始碼如 「視窗10」 可以有逾400 萬檔案 和500 GB 位元組 (圖264)。若不提供原始碼,程式專家們肯定不知於程式那處作適當修改。
(圖264) 「視窗 10」檔案大小
若需要修改原始碼失掉之軟件程式便要進行逆向工程步驟。軟件逆向工程涉及基於二進制機械語言逆向改寫為程式之原始碼。改良或恢復編寫程式便需要獲取其原始碼。一則可以修正程式錯誤,二則可以辨認惡意植入之程式病毒。軟件程式逆向工程目的若為抄襲或複製便產生侵犯版權問題。軟件程式逆向工程不僅極為複雜,也化大量金錢而通常得不償失。
(ii) 硬件正向/逆向工程
晶片 (IC) 和系統單晶片 (SoC,System-on-a Chip) 製作產業
廣義地說,硬件逆向工程是把一件電腦設備折散,理解它是如何運作。舉個例子:有廠商想要知道競爭對手之中央處理器如何運作,便購買了一台,完全折散它,跟著造一款一模一樣之CPU。不過這行為大部份國家都視作非法。事實上硬件逆向工程不僅化錢,更需要專門技術。為什麼不直接向代理商購買?
晶片組產業正向工程大致可分為兩類:(i) 整合元件製造 (IDM,Integrated Design and Manufacture) (ii) 代工生產 (OEM,Original Equipment Manufacture) 。
(1) 整合元件製造 (IDM)
英文縮寫 IDM要點放在字母 M,即製造,設計和其他工序不可以製造產品。整合元件製造一詞解作廠商把 IC之設計、晶片製造、包裝和測試集於一身,全部自家承辦。當半導體IC產業還處於不十分先進年代,整合元件製造是那時普遍採用之工序。傳統IC品牌 Intel 公司之桌上電腦 「Intel CPU」 便是IDM行業例子之表表者。
現時智能手機當道,每人都一機在手,令 Intel 或其他桌上電腦IDM廠家只可以分享廣大電子市場一小份額,絕大份額都給生產智能手機內置之先進及複雜晶片組廠家佔據了。基於生態系統環境及成本效益誘因,智能手機晶片組廠家不會採用IDM工序生產極之精準及超小型主晶片組。分工合作生産優勝過一家承辦。智能手機主晶片組分別由 (i) 軟件輔助晶片電路設計、 (ii) 光刻、(iii) 蝕刻、(iv) 硅晶圓片生產、(v) 包裝和 (vi) 測試,由不同廠家承辦。生產一環,即工序 (ii) 至 (iv) 叫代工生産 (OME) ,是整個産業主要環節。
(2) 代工生産 (OEM)
(a) EUV 光刻蝕和代工生產
桌上電腦主板機安放了CPU,graphic card, RAM 槽等等 (圖265)。但智能手機不可以承受如此空間奢侈。主晶片組 (chipset) 一定要包括主要線路組成並要造得非常細小。智能手機之「腦」, 即系統單晶片 (SoC chipset,System-on-a-Chip),便是廠家把各主要組成如 CPU,GPU,記憶體,通用序列匯流排控制器 (USB controller),電源管理組,無線接收組如 WiFi、 3G、 4G LTE、5G、藍牙等等一體化地刻在一細小硅晶片上 (圖266)。
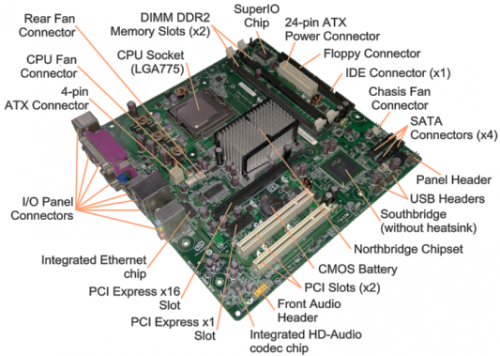 |  |
(圖265) 桌上電腦主板機布局 | (圖266) 麒麟970 智能手機系統單晶片 |
怎樣才可以生産如此精密之系統單晶片?首先交由電路設計工程師完成晶片設計 (需要軟件輔助) 。跟着涉及兩層次工序:(i) 納米級 (nm, 即 10-9 m) 光刻蝕和 (ii) 代工生產 (OEM,Original Equipment Manufacture) 嵌入各組件製成晶圓片。現今世界上只有一家「公司」有能力製造極高工藝水平之EUV (Extreme Ultraviolet,13.3 – 13.7 nm 電磁波段) 光刻機 (圖267),於2019年已達致 7 nm 光刻規格。 下列流程簡介EUV光刻蝕工藝程序:
 |  |  | 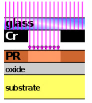 | |||
(i) Preparation of wafer | (ii) Application of photoresist | (iii) Alignment of photomask | (iv) Exposure to EUV |
 |  | 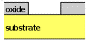 | ||
(v) Development and removal of photoresist exposed to EUV | (vi) Etching of exposed oxide | (vii) Removal of remaining photoresist |
按晶片組設計複雜程度,重複步驟 (iii) 至 (vi) 。
這家獨佔鰲頭EUV光刻機製造商總部在荷蘭,叫ASML (Advanced Semiconductor Materials International) Holding of the Netherlands. 事實上這家由數大垮國企業提供技術支援,用家財力支持之「公司」只銷售技術,售賣光刻機,不造晶片組製成品。製造商和用家一起成為持份者。

(圖 267) 製造 7 nm 系統單晶片開拓者,一台ASML EUV 光刻機
在2019年,除了裝運到三星和英特爾,一半ASML輸出之26台EUV光刻機都去了台積電 (TSMC, Taiwan Semiconductor Manufacturing Company Ltd.) 為各大手機生產商做代工 (OEM,Original Equipment Manufacture) 生產 7 nm SoC chipset圓晶片,例如蘋果iphone 12 之A14 Bionic、華為 Mate 30之 Kirin 990 5G或三星 Galaxy S20之高通Snapdragon 865。這些極細小硅層架構之晶體管總量每平方毫米密度可高達一億個級數。
没有一間規模龐大垮國手機生產商有能力可以繞過這 (光刻蝕 – 代工) 資訊科技官僚體制運作,自行一家公司一手正向工序,生產4G或5G智能手機之主晶片組。總之,智能手機SoC chipset逆向工程眼前只是夢想,行不通的。
捷足先登,或俗語之 「贏在起跑線」, 或英諺語之 “Early bird catches the worm” ,都示意最先發明者最有機會掌握隨著之發展。基於掌握最先進光刻機工藝核心技術,ASML緊握硅基SoC主晶片組OME量產之樽頸位。
(b) 乾法蝕刻 (Dry etching) – 反應離子蝕刻 (Reactive Ion Etching,RIE) 和深反應離子蝕刻 (Deep Reactive Ion Etching,DRIE)工藝 (基於網上資料)
EUV光刻後段工藝是蝕刻,一般採用化學方法蝕去硅基質上不要之氧化物 (濕法蝕刻)。另一種蝕刻方法是乾法蝕刻 (Dry etching) 。目前乾法蝕刻採用反應離子蝕刻 (Reactive Ion Etching,RIE) 工藝。它利用高能等離子 (電漿體) 強化後的氣體束轟擊目標晶圓片,達到蝕刻目的。RIE蝕刻率競爭力不太強。近年開發了深反應離子蝕刻 (Deep Reactive Ion Etching,DRIE) 工藝,採用兩個射頻源:將等離子的產生和自偏壓的產生分離,有效避免了RIE蝕刻中射頻功率和等離子密度之間的矛盾。能夠實現可控的側向蝕刻,可以製作出陡峭或其他傾斜角度的側壁。DRIE工藝步驟(Bosch工藝):鈍化—蝕刻—鈍化—蝕刻—。
How are microchips made
(3) IDM 模式製造 SoC Chipset
當在低晶體密度 IC 工藝年代,生產商一般採用 IDM 工序。現在極高晶體密度 IC 如SoC 主晶片組,整個製造流程都不可能由單一垮國企業承辦。晶片設計、光刻、蝕刻、包裝和測試是由不同製造商承辦。這不是經濟貿易問題,而是由於要批付眾多專利權和克服極高要求工藝如光刻工序,並不是某一大廠家可以自家應付得來。因此出現了代工製造 (OEM) 微工序生產行業,分工合作製造SoC主晶片組。
中國經數十年改革開放發展,至2019年,與美國地緣政治實力變化激發巨大差異。美國要遏制中國國力崛起,起初只是互相提升貿易關稅壁壘,後再因中國在潛有巨大商機和軍備發展之5G網絡通訊建設取得國內外快速發展,極有機會主導全球5G通訊建設標準。基於恐懼微電子高科技領域優勢消失,美國因此瞄準堵截SoC 主晶片組代工製造環節,即中國 SoC 主晶片組製造弱項,作為弄糟中國之5G發展。接着華為發現不可以從ASML輸入EUV光刻機和找台積電代工5G 麒麟系列SoC 主晶片組。不過華為也即時發馬後炮向聯發科技 (Media Tek Inc,MTK,也要台積電代工) 購入1.2億天璣 (Dimensity) 芯片作儲備,為未來兩年5G手機SoC芯片做備胎。
2020年中國反擊,定下 「雙經濟循環」政策 (主要應付新冠肺炎疫情國內受控國外糾纏下之後續世界新經濟情況) ,其中一環節致力於攻克IDM製造nm工藝SoC主晶片組之高科技要求。例如力挺中芯國際OEM量產nm晶圓片。以當前國力而言,從長遠的觀點來說,克服EUV光刻工藝這弱項是有望成功的。2020 中國科學院蘇州納米技術與納米仿生研究所 (中科院蘇州納米所,CAS- SINANO)研發雙激光無掩模納米級光刻工藝,有別於ASML之EUV photoresist masking光刻工藝。有希望數年時間後可以擺脫ASML制肘,主自IDM生產nm級數SoC 主晶片組,應付智能手機功能日新月異之市場要求。
2020年傳統IC品牌 Intel 公司宣告自主 IDM 7 nm晶片生產計劃,不用外工OEM廠商如台積電或三星。但嘗試也不是一帆風順。
(4) “碳基電子邏輯閘” 和 “分子邏輯閘電路” 之開發
最新探究之「碳基電子邏輯閘」(網上搜尋) 很有可能取代硅基電子邏輯閘,發展為另一途徑生產先進 SoC chipset。2020中科院團隊分別成功研製石墨烯基質高速半導體和石墨烯單晶晶圓。有鑒於目前或將來科技都極難克服1 nm或小於1 nm光刻技術,硅基SoC主晶片組研發至2 nm光刻階段很可能會停頓下來。那時後硅基 SoC主晶片組年代智能手機市場將會由碳(石墨烯)基 SoC主晶片組廠商主導。從企業家角度看,若生產線開始建基於硅基微組裝,則沒有可能改為碳基微組裝,因為所有設施皆用硅基技術,就算要面對死胡同也要面對。
China’s endeavor in carbon-based chip development
另一可能預見的進展是實現 “分子邏輯閘電路”,無界面耦合人體器官,進行各類前所未有之醫療療程 。目前硅基SoC系統單晶片設施如何微型複雜化也不可能無界面植入人體器官 (回顧 28-29頁: 神祕的人腦記憶機理)。
9.4電子製作:數字頻率顯示器
數字電子顯示往往令人想起 0至 9之各種變化。當我們掌握了各類電子零件使用技巧後,便可以計設一電路滿足這方面要求。換句話說,就是裝組一數字頻率顯示器。顯示0至9數字之各種變化。電路可分拆為三部份 (模塊) ,在麵飽板上完成裝坎。
(1) 第一模塊為時鐘產生器,提供時基。
(2) 第二模塊把產生之 (0 1) 頻率時基配合一枚 IC (CD 4510),輸出 BCD (Binary Coded Decimal),即 4-bit 訊號。
(3) 第三模塊採用 IC CD 4511,轉 BCD 4-bit 訊號輸入為 abcdefg 7-bit 輸出,再由abcdefg 7-bit 推動7 節目字形LED 作數字顯示。
整體線路 (模塊化)
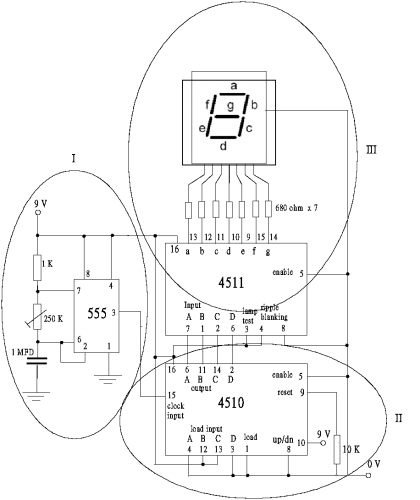 |
| (圖 268) 0至9數字頻率顯示模塊電路 |
(i) 模塊 (1) – 555無穩態振盪器
首先需要一個時基。555 IC 是專為產生時基而設計,廣受用家歡迎。線路需要一個數 Hz 自發脈衝訊號。第一模塊線路之 555 IC、1K (Ra)、250 K (Rb) 可變電阻和 1mF (C) 電容組成無穩態 (即自發) 振盪,頻率為 f = [1.443/ (Ra + 2Rb) (C)] Hz 。
時基頻率變動一般採用改變 Rb 之阻值方法而不是改變電容 C 之大小容量。以 (圖 269) Ra = 1000Ω,Rb 可變電阻 = 250 KΩ ,C = 1mF 代入公式計算,LED 光暗頻率可調校由 1443 Hz 至 2.88 Hz。.
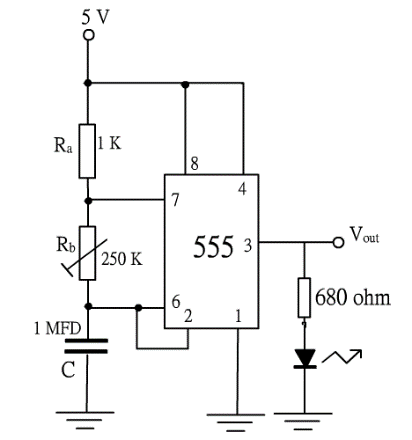
(圖 269) LED光暗脈衝頻率顯示
注意:
(a) 不建議一開始便接好整個數字頻率顯示器電路。應一模塊一模塊地連接並測試。先接好第一模塊線路,檢測555輸出 (圖269)。看看輸出LED有否起振。
(b) 555電源是 5 V。9 V電源會燒燬單一LED,也影響輸出頻率。

555 ocillator
(ii) 模塊 (2) -加入 CD 4510 BCD 4-bit計數器
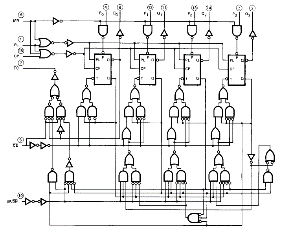
(圖 270) CD 4510內部結構
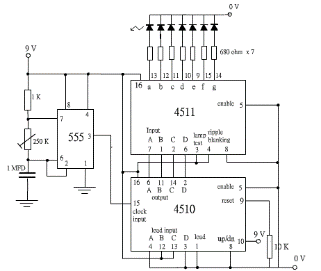 |
(圖 271) 4 個獨立 LED顯 示 ABCD 輸出 |

CD 4510 BCD4 bit output
接着把起振模塊 (1) 連接模塊 (2),即 BCD 4-bit 計數器。555 第3和4腳分別接CD 4510 第15和16腳。CD 4510 是一枚 BCD 計數器,會按脈衝輸入演繹成 BCD 編碼 (圖 268),輸出 4-bit (ABCD) 位元組,其真值表如下
| 脈衝 | CD 4510 (BCD counter) 輸出 0表示暗,1表示光 | |||
| A | B | C | D | |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 |
| 5 | 1 | 0 | 1 | 0 |
| 6 | 0 | 1 | 1 | 0 |
| 7 | 1 | 1 | 1 | 0 |
| 8 | 0 | 0 | 0 | 1 |
| 9 | 1 | 0 | 0 | 1 |
| 10 | 0 | 0 | 0 | 0 |
(iii) 模塊 (3) -加入轉 BCD 輸入為 abcdefg 7-bit 輸出
接着把ABCD 4-bit轉為abcdefg 7-bit輸出,作用是推動7節目形 LED 顯示 0至9數字。其布林真值表為:
| BCD 輸入 | 7 節輸出 | |||||||||
| A | B | C | D | a | b | c | d | e | f | g |
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 |
轉化需要軟件演繹。但因其使用太普遍,廠家把程式轉為硬件,以CMOS IC 出售。CD 4511 BCD to 7-segment CMOS 便是這用途之表表者。
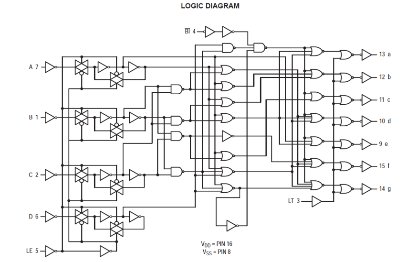
(圖 272) CD 4511 內部結構
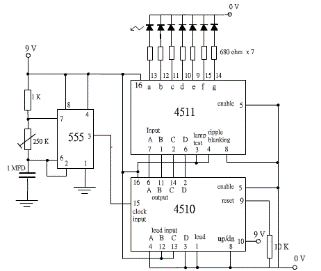
(圖 273) 7個獨立LED顯示 abcdefg 7-bit 輸出
(iv)模塊 (3)續 – 轉abcdefg 7-bit 輸出為7節日字 LED 數字顯示
最後要把 abcdefg 7-bit 輸出點亮 7 節日字形 LED,顯示數字。7 節日字形 LED 有共陽極和共陰極兩類,有紅色或綠色選擇。
 | 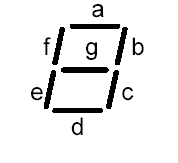 |
| 0.56” 共陰極 7 節日字形 LED 第 3 或 8 腳接 0 V,3 V接第 1 腳點亮 e 節,第 2 腳點亮 d 節,第 4 腳點亮 c 節,第 5 腳點亮句號,第 6 腳點亮 b 節,第 7 腳點亮 a 節,第 9 腳點亮 f 節,第 10 腳點亮 g 節。 | |||||||||
| 7節輸出 | 數字顯示 | ||||||||
| a | b | c | d | e | f | g | |||
| 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | ||
| 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | ||
| 1 | 1 | 0 | 1 | 1 | 0 | 1 | 2 | ||
| 1 | 1 | 1 | 1 | 0 | 0 | 1 | 3 | ||
| 0 | 1 | 1 | 0 | 0 | 1 | 1 | 4 | ||
| 1 | 0 | 1 | 1 | 0 | 1 | 1 | 5 | ||
| 0 | 0 | 1 | 1 | 1 | 1 | 1 | 6 | ||
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | 7 | ||
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 8 | ||
| 1 | 1 | 1 | 0 | 0 | 1 | 1 | 9 | ||
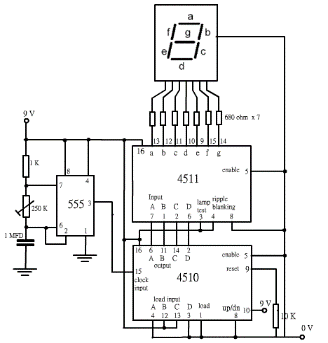
(圖 274) 完整之7 節 LED 連續顯示 0 至 9 數字線路

(圖 275) abcdefg 7-bit 推動 7 節 LED 顯示
實時方形脈衝訊號輸出如下圖:
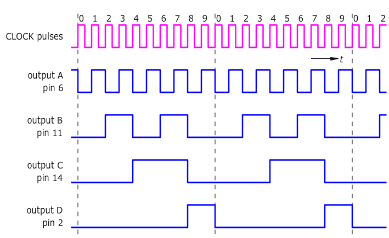 |
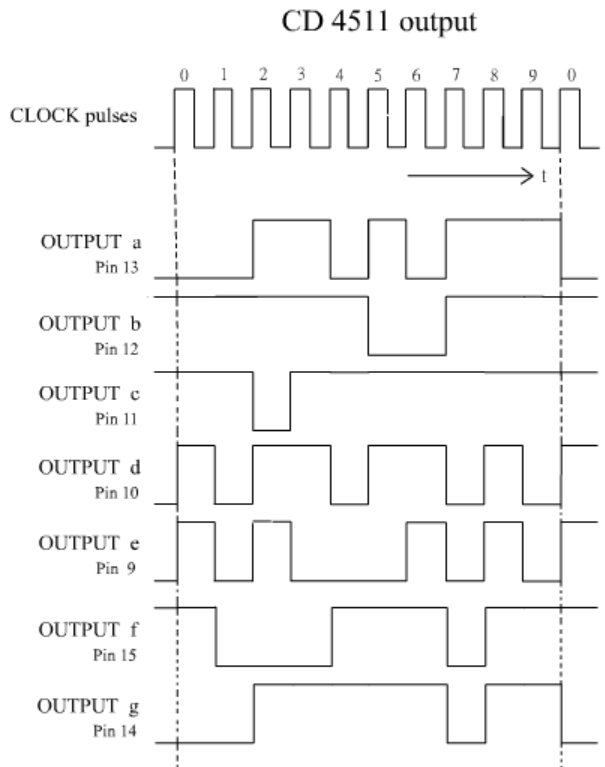
上圖可如下理解:
0 脈衝 :開始振盪 CD 4510 輸出端為 (0 0 0 0),CD 4511輸出端為 (1 1 1 1 1 1 0)
第1脈衝:CD 4510 輸出端為 (1 0 0 0),CD 4511輸出端為 (0 1 1 0 0 0 0)
第2脈衝:CD 4510 輸出端為 (0 1 0 0),CD 4511輸出端為 (1 1 0 1 1 0 1)
第3脈衝:CD 4510 輸出端為 (1 1 0 0),CD 4511輸出端為 (1 1 1 1 0 0 1)
第4脈衝:CD 4510 輸出端為 (0 0 1 0),CD 4511輸出端為 (0 1 1 0 0 1 1)
第5脈衝:CD 4510 輸出端為 (1 0 1 0),CD 4511輸出端為 (1 0 1 1 0 1 1)
第6脈衝:CD 4510 輸出端為 (0 1 1 0),CD 4511輸出端為 (0 0 1 1 1 1 1)
第7脈衝:CD 4510 輸出端為 (1 1 1 0),CD 4511輸出端為 (1 1 1 0 0 0 0)
第8脈衝:CD 4510 輸出端為 (0 0 0 1),CD 4511輸出端為 (1 1 1 1 1 1 1)
第9脈衝:CD 4510 輸出端為 (1 0 0 1),CD 4511輸出端為 (1 1 1 0 0 1 1)
整個流程如下圖:
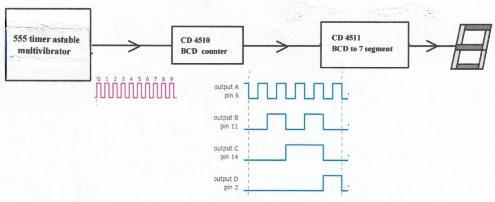
4510 第8腳 (up/down) 可提供由 0至9連續由低至高顯示,即第 8 腳接地 (0),或由9至0連續由高至低顯示,即第8腳接電源9V。
Up-counting 0 to 9
Down-counting 9 to 0
改變250 KΩ 可變阻阻值可調高數字顯示頻率。
Varying speed counting 0 to 9
數字顯示脈衝頻率對初學者可說不簡單,不能以單一線路完成。不過正是如此,所有數字電路都應如此分析。基夲上,所有數字線路只是關乎高/低壓電子開/關和一脈衝時基之複雜關係。